Fortran Object oriented Ordinary Differential Equations integration library
Find us on…
FOODIE
FOODIE
FOODIE, Fortran Object-Oriented Differential-equations Integration Environment
- FOODIE is a pure Fortran (KISS) library providing an awesome environment for the numerical integration of Differential-equations (ODE, PDE);
- FOODIE is Fortran 2008+ standard compliant;
- FOODIE is OOP designed;
- FOODIE is a Free, Open Source Project.
Table of Contents
What is FOODIE?
Modern Fortran standards (2003+) have introduced support for Object-Oriented Programming (OOP). Exploiting new features like Abstract Data Type (ADT) is now possible to develop a KISS library providing an awesome environment for the numerical integration of Differential-equations such as Ordinary and Partial Differential Eqautions (ODE, PDE). FOODIE is tailored to the systems arising from the semi-discretization of PDEs, but it is not limited to them.
The FOODIE environment allows the (numerical) solution of general, non linear differential equations system of the form:
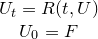
where:
- U_t = dU/dt;
- U is the vector of state variables being a function of the time-like independent variable t;
- R is the (vectorial) residual function, it could be a non linear function of the solution U itself;
- F is the (vectorial) initial conditions function.
The FOODIE has two main purposes:
- for developers devising new schemes for the numerical integrations of differential equations (DE):
- provide a concise, clear, robust and comprehensive abstract environment by means of which:
- express the solvers formulae with a very high-level language, it being close as much as possible to their natual mathematical formulations; this ensures:
- clearness, conciseness and robustness;
- fast-developing;
- express the solvers formulae with a very high-level language, it being close as much as possible to their natual mathematical formulations; this ensures:
- provide a concise, clear, robust and comprehensive abstract environment by means of which:
- for clients that must solve a differential equations system:
- provide a simple, standard API for many built-in DE solvers out-of-the-box, thus allowing:
- fast-solution of new problems;
- robustness: the same DE solver is applied to different problems, i.e. cross-validation;
- provide a simple, standard API for many built-in DE solvers out-of-the-box, thus allowing:
Go to Top
Main features
FOODIE is aimed to be a KISS-pure-Fortran library for integrating Ordinary Differential Equations (ODE), it being:
- Pure Fortran implementation;
- KISS and user-friendly:
- simple API, presently based on the Rouson's Abstract Data Type Pattern [8];
- easy building and porting on heterogeneous architectures;
- comprehensive solvers set out-of-the-box:
- explicit schemes:
- Adams-Bashforth schemes see [7, 12]:
- 1 step, namely the forward explicit Euler scheme, 1st order accurate;
- 2 to 16 steps, 2nd to 16th accurate, respectively;
- Euler (forward explicit) scheme, 1st order accurate;
- Leapfrog, 2nd order accurate:
- unfiltered leapfrog, 2nd order accurate, mostly unstable, see [4];
- Robert-Asselin filtered leapfrog, 1st order accurate, see [4, 5, 6];
- Robert-Asselin-Williams filtered leapfrog, 3rd order accurate, see [5, 6];
- Linear Multistep Methods, SSP schemes see [16]:
- 3 steps, 2nd order accurate;
- 4 steps, 3rd order accurate;
- 5 steps, 3rd order accurate;
- Linear Multistep Methods, SSP with Variable Step Size (VSS) schemes see [17]:
- 2 steps, 2nd order accurate;
- 3 steps, 2nd order accurate;
- 3 steps, 3rd order accurate;
- 4 steps, 3rd order accurate;
- 5 steps, 3rd order accurate;
- Linear Multistep Runge-Kutta Methods SSP schemes see [18]:
- 2 steps, 2 stages, 3rd order accurate;
- 3 steps, 2 stages, 3rd order accurate;
- 4 steps, 3 stages, 5th order accurate;
- 3 steps, 6 stages, 5th order accurate;
- 3 steps, 5 stages, 6th order accurate;
- 3 steps, 7 stages, 7th order accurate;
- 4 steps, 7 stages, 7th order accurate;
- 4 steps, 5 stages, 8th order accurate;
- 5 steps, 9 stages, 8th order accurate;
- 4 steps, 9 stages, 9th order accurate;
- 3 steps, 20 stages, 10th order accurate;
- Runge-Kutta schemes:
- [+] Linear SSP (of any order) schemes, see [16]:
- generic s-stages of order (s-1)-th;
- generic s-stages of order s-th;
- low-storage schemes, see [1, 2, 3]:
- 1 stage, namely the forward explicit Euler scheme, 1st order accurate;
- 2 stages;
- 3 stages;
- 4 stages;
- 5 stages, 4th order accurate, 2N registers, see [3];
- 6 stages, 4th order accurate, 2N registers, see [9];
- 7 stages, 4th order accurate, 2N registers, see [9];
- 12 stages, 4th order accurate, 2N registers, see [10];
- 13 stages, 4th order accurate, 2N registers, see [10];
- 14 stages, 4th order accurate, 2N registers, see [10];
- TVD/SSP schemes, see [1]:
- 1 stage, namely the forward explicit Euler scheme, 1st order accurate;
- 2 stages, 2nd order accurate;
- 3 stages, 3rd order accurate;
- 4 stages;
- 5 stages, 4th order accurate;
- embedded (adaptive) schemes:
- Heun-Euler, 2 stages, 2nd order accurate;
- Runge-Kutta-Fehlberg, 5 stages, 4th order accurate;
- Runge-Kutta-Cash-Karp, 6 stages, 5th order accurate, see [13];
- Prince-Dormand, 7 stages, 4th order accurate, see [11];
- Calvo, 9 stages, 6th order accurate, see [14];
- Feagin, 17 stages, 10th order accurate, see [15];
- [+] Linear SSP (of any order) schemes, see [16]:
- Adams-Bashforth schemes see [7, 12]:
- implicit schemes:
- Runge-Kutta schemes;
- Adams-Moulton schemes:
- 0 step, 1st order accurate;
- 1 step, 2nd accurate;
- 2 steps, 3rd accurate;
- 3 steps, 4th accurate;
- Backward Differentiation Formula schemes:
- 1 step, namely the backward implicit Euler scheme, 1st order accurate;
- 2 to 6 steps, 2nd to 6th accurate, respectively;
- predictor-corrector schemes:
- Adams-Bashforth-Moulton schemes:
- 1 step, AB(1)-AM(0), 1st order accurate;
- 2 steps, AB(2)-AM(1), 2nd accurate;
- 3 steps, AB(3)-AM(2), 3rd accurate;
- 4 steps, AB(4)-AM(3), 4th accurate;
- Adams-Bashforth-Moulton schemes:
- explicit schemes:
- efficient and non intrusive:
- FOODIE environment is unaware of any eventual parallel paradigms the clients used, but it is proved to preserve high scalability on parallel architectures such as:
- OpenMP directive-based codes on shared memory multi/many cores architectures;
- CoArray Fortran (CAF) based codes for Partitioned Global Address Space (PGAS) programming model;
- MPI based code on distributed memory clusters;
- GPGPU/accelerators device enabled codes;
- FOODIE environment is unaware of any eventual parallel paradigms the clients used, but it is proved to preserve high scalability on parallel architectures such as:
- Tests-Driven Developed (TDD):
- well documented:
- clear documentation of schemes implementations, e.g. see Adams-Bashforth API documentation;
- complete API reference;
- comprehensive wiki:
- collaborative developed on GitHub;
- FOSS licensed;
Any feature request is welcome.
Bibliography
[1] High Order Strong Stability Preserving Time Discretizations, Gottlieb, S., Ketcheson, D. I., Shu, C.W., Journal of Scientific Computing, vol. 38, N. 3, 2009, pp. 251–289.
[2] Low-Storage Runge-Kutta Schemes, J. H. Williamson, Journal of Computational Physics, vol. 35, 1980, pp. 48–56.
[3] Fourth-Order 2N-Storage Runge-Kutta Schemes, Mark H. Carpenter, Christopher A. Kennedy, NASA Technical Memorandum 109112, June 1994.
[4] Numerical methods used in atmospheric models, Mesinger F. and A. Arakawa, Global Atmospheric Research Programme (GARP), Technical Report, 1976.
[5] A Proposed Modification to the Robert-Asselin Time Filter, Williams, P. D., Mon. Wea. Rev., vol. 137, pp. 2538–2546, 2009, doi: http://dx.doi.org/10.1175/2009MWR2724.1.
[6] The RAW filter: An improvement to the Robert-Asselin filter in semi-implicit integrations, Williams, P.D., Monthly Weather Review, vol. 139(6), pages 1996–2007, June 2011.
[7] Linear multistep method, wikipedia article.
[8] Scientific Software Design: The Object-Oriented Way, Rouson, Damian and Xia, Jim and Xu, Xiaofeng, 2011, ISBN 9780521888134, Cambridge University Press, New York, NY, USA.
[9] High-accuracy large-step explicit Runge–Kutta (HALE-RK) schemes for computational aeroacoustics, Vasanth Allampalli and Ray Hixon and M. Nallasamy and Scott D. Sawyer, Journal of Computational Physics, vol. 228, 2009, pp. 3837–3850.
[10] Efficient low-storage Runge–Kutta schemes with optimized stability regions, Jens Niegemann and Richard Diehl and Kurt Busch, Journal of Computational Physics, vol. 231, 2012, pp. 364–372.
[11] A family of embedded Runge-Kutta formulae, Dormand, J. R.; Prince, P. J. (1980), , Journal of Computational and Applied Mathematics 6 (1): 19–26, doi:10.1016/0771-050X(80)90013-3.
[12] Cowell Type Numerical Integration As Applied to Satellite Orbit Computation, J. L. Maury Jr., G. P. Segal, X-553-69-46, April 1969, NASA-TM-X-63542.
[13] A variable order Runge-Kutta method for initial value problems with rapidly varying right-hand sides, J. R. Cash, A. H. Karp, ACM Transactions on Mathematical Software, vol. 16, pp. 201–222, 1990, doi:10.1145/79505.79507.
[14] A New Embedded Pair of Runge-Kutta Formulas of orders 5 and 6, M. Calvo, J.I. Montijano, L. Randez, Computers & Mathematics with Applications, Volume 20, Issue 1, 1990, Pages 15–24, ISSN 0898-1221, http://dx.doi.org/10.1016/0898-1221(90)90064-Q.
[15] A tenth-order Runge-Kutta method with error estimate, Feagin, T., Proceedings of the IAENG Conf. on Scientific Computing. 2007.
[16] Strong Stability Preserving Runge-Kutta and Multistep Time Discretizations, S. Gottlieb, D. Ketcheson, C.W. Shu, 2011, 978-981-4289-26-9, doi:10.1142/7498, World Scientific Publishing Co. Pte. Ltd.
[17] Strong Stability Preserving Explicit Linear Multistep Methods with Variable Step Size, Y. Hadjimichael, D. Ketcheson, L. Lóczi, A. Németh, 2016, SIAM J. Numer. Anal., 54(5), 2799–2832.DOI:10.1137/15M101717X.
[18] Explicit Strong Stability Preserving Multistep Runge-Kutta Methods, C. Bresten, S. Gottlieb, Z. Grant, D. Higgs, D. Ketcheson, A. Nemeth, Mathematics of Computation, 2016, http://dx.doi.org/10.1090/mcom/3115.
Go to Top
Status 
FOODIE project is young, but developed with love. Many integrators have been implemented using the Rouson's Abstract Data Type Pattern and tested with complex problems, but the library API is still in beta testing status. Nevertheless, FOODIE is already proven to be able to integrate a wide range of different ODE problems, from pure ODEs (Lorenz and inertial oscillations equations) to complex PDEs (Burgers and Euler equations), see the documentation.
We are searching for Fortraners enthusiast joining our team!
Copyrights
FOODIE is an open source project, it is distributed under a multi-licensing system:
- for FOSS projects:
- GPL v3;
- for closed source/commercial projects:
- BSD 2-Clause;
- BSD 3-Clause;
- MIT.
Anyone is interest to use, to develop or to contribute to FOODIE is welcome, feel free to select the license that best matches your soul!
More details can be found on wiki.
Go to Top
Documentation
Besides this README file the FOODIE documentation is contained into its own wiki. Detailed documentation of the API is contained into the GitHub Pages that can also be created locally by means of ford tool.
Go to Top
Source Files
Modules
- foodie
- foodie_error_codes
- foodie_integrand_object
- foodie_integrator_adams_bashforth
- foodie_integrator_adams_bashforth_moulton
- foodie_integrator_adams_moulton
- foodie_integrator_backward_differentiation_formula
- foodie_integrator_euler_explicit
- foodie_integrator_leapfrog
- foodie_integrator_lmm_ssp
- All modules…






